Vectores linha e coluna são casos especiais de matrizes. Uma matriz 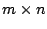 é conjunto de valores dispostos por m linhas e m colunas. Para delimitar as matrizes são normalmente usados parêntesis rectos ou curvos, para normalizar vamos usar os rectos. Por exemplo, quando
é conjunto de valores dispostos por m linhas e m colunas. Para delimitar as matrizes são normalmente usados parêntesis rectos ou curvos, para normalizar vamos usar os rectos. Por exemplo, quando 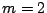 e
e 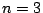 temos uma matriz tal como:
temos uma matriz tal como:
que para ser introduzida no Matlab insere-se linha após linha seguindo a mesma sintaxe dos vectores:
» A = [5 7 9
1 -3 7]
A =
5 7 9
1 -3 -7
Outra forma é separando as linhas com ';' em vez de novas linhas:
» B=[1 2 5; 0 3 9]
B =
1 2 5
0 3 9
» C = [0, 1; 3, -2; 4, 2]
C =
0 1
3 -2
4 2
» D = [1:5; 6:10; 11:2:20]
D =
1 2 3 4 5
6 7 8 9 10
11 13 15 17 19
Assim A e B são matrizes 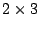 , C é uma matriz
, C é uma matriz 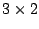 e D é
e D é 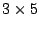 . Neste contexto um vector coluna é uma matriz
. Neste contexto um vector coluna é uma matriz 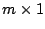 e um vector linha
e um vector linha 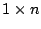 .
.
Subsecções
Rodrigo Maia
2003-10-07
![]() , C é uma matriz
, C é uma matriz ![]() e D é
e D é ![]() . Neste contexto um vector coluna é uma matriz
. Neste contexto um vector coluna é uma matriz ![]() e um vector linha
e um vector linha ![]() .
.