Figura 6:
Gráficos do Exemplo ![[*]](file:/usr/share/lib/latex2html/icons/crossref.png)
|
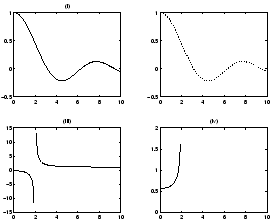 |
» x = 0:0.1:10;
» y = sin(x)./x;
Warning: Divide by zero
» subplot(221), plot(x,y), title('(i)')
» u = 1./(x-1).^2 + x;
Warning: Divide by zero.
» subplot(222),plot(x,u), title('(ii)')
» v = (x.^2+1)./(x.^2-4);
Warning: Divide by zero.
» subplot(223),plot(x,v),title('(iii)')
» w = ((10-x).^(1/3)-1)./sqrt(4-x.^2);
Warning: Divide by zero.
» subplot(224),plot(x,w),title('(iv)')
Warning: Imaginary parts of complex X and/or Y arguments ignored.
Tenha atenção ao repetido uso dos operadores ponto ``ponto-multiplicação'', ``ponto-divisão'', ``ponto-potência''. Podemos fazer algumas modificações de forma a tornar os gráficos mais legíveis, aplicar alguns comandos já estudados:
» subplot(222),axis([0 10 0 10])
» grid
» grid
» hold on
» plot(x,v,'-'), hold off, plot(x,y,':')
Exercício 13.1
Insira os seguintes vectores:
- Quais dos produtos:
U*V, V*W, U*V', V*W', W*Z', U.*V
U'*V, V'*W, W'*Z, U.*W, W.*Z, V.*W
são permitidos? Indique quais dos resultados permitidos resultam em vectores linha e coluna e apresente os resultados.
- Ponha na forma de uma tabela (abcissas,ordenadas) as funções:
e
para
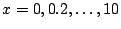 . Faça o mesmo para:
. Faça o mesmo para:
e esboce o seu gráfico para o intervalo
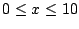 .
.
Rodrigo Maia
2003-10-07
![\begin{displaymath}\begin{array}{cc}
\vec{U} = \left[\begin{array}{cccc}6&2&4&1...
...egin{array}{c}-1 -5 -2 -3\end{array}\right]
\end{array}\end{displaymath}](img73.png)