next up previous contents
Seguinte: 14.12 Sistemas de Equações Acima: 14 Matrizes Anterior: 14.10 Produto Matriz-Vector   Conteúdo

14.11 Produtos Matriz-Matriz

Para formar o produto entre uma matriz A 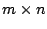$m\times n$ e uma matriz B 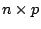$n\times p$, denotado por 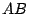$AB$, podemos visualizar a primeira matriz (A) composta por m vectores linha de comprimento n colocados uns por cima dos outros enquanto a segunda (B) é composta por p vectores coluna de comprimento n:

\begin{displaymath}A=m\mathrm{(linhas)}\left\{\left[\begin{array}{c}\fbox{\hspac... ...m}{2cm}}\end{array}\right]}_{{\normalsize p\mathrm{(colunas)}}}\end{displaymath}

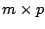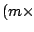
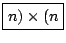
O elemento na i-ésima linha e da j-ésima coluna do produto é o produto escalar entre a i-ésima linha de A e a j-ésima coluna de B. A matriz-produto resultante é uma 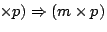$m\times p$ : $(m\times\!$ \fbox{$n)\times(n$} $\!\times p)\Rightarrow(m\times p)$ Uma forma de testar a percepção deste conceito calcular manualmente os seguintes exemplos executados com o Matlab :

»  A = [5 7 9; 1 -3 -7]

A =

     5     7     9
     1    -3    -7

» B = [0, 1; 3, -2; 4, 2]

B =

     0     1
     3    -2
     4     2

» C = A*B

C =

    57     9
   -37    -7

» D = B*A

D =

     1    -3    -7
    13    27    41
    22    22    22

»  E = B'*A'

E =

    57   -37
     9    -7

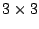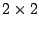Como se constata 'E'=C' o que indica que '(A*B)'=B'*A'' Porque razão 'B*A' é uma matriz $3\times 3$ e 'A*B' é $2\times 2$?

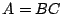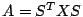Exercício 14.1   Às vezes é necessário factorizar uma matriz, p. ex. $A=BC$ ou $A=S^TXS$ onde é requerido que os factores tenham determinadas propriedades específicas. Use o comando 'lookfor palavra-chave' para obter uma lista dos comandos de factorização do Matlab .

next up previous contents
Seguinte: 14.12 Sistemas de Equações Acima: 14 Matrizes Anterior: 14.10 Produto Matriz-Vector   Conteúdo
Rodrigo Maia 2003-10-07