Seguinte: 15 Caracteres, Expressões de Acima: 14 Matrizes Anterior: 14.11 Produtos Matriz-Matriz Conteúdo
De uma forma geral um sistema de equações lineares pode ser expresso em termos de uma matriz de coeficientes A, um vector de termos b e um vector de incógnitas x:
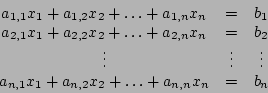
Quando A é não-singular e quadrada (![]() ), ou seja que o número de equações independentes é igual ao número de incógnitas, o sistema tem uma solução única dada por:
), ou seja que o número de equações independentes é igual ao número de incógnitas, o sistema tem uma solução única dada por:
Esta aproximação baseada na matriz inversa, apesar de formalmente correcta é ineficiente para aplicações práticas (onde o número de equações pode ser extremamente elevado) e pode conduzir a erros numéricos consideráveis a não ser que sejam utilizadas técnicas apropriadas. Varias soluções técnicas, eficientes e estáveis, têm sido desenvolvidas para resolver sistemas de equações lineares e o mais apropriado a cada situação dependerá das características da matriz dos coeficientes (![]() ). Por exemplo, se esta é ou não simétrica, ou é positiva definida ou se tem uma estrutura particular (esparsa ou completa). O Matlab está equipado com muitas destas técnicas na sua biblioteca de rotinas que são chamadas automaticamente.
). Por exemplo, se esta é ou não simétrica, ou é positiva definida ou se tem uma estrutura particular (esparsa ou completa). O Matlab está equipado com muitas destas técnicas na sua biblioteca de rotinas que são chamadas automaticamente.
A rotina standard do Matlab para resolver sistemas de equações lineares é invocada pelo uso da divisão matricial à esquerda ![]() :
:
![\begin{displaymath}
A=
\left[
\begin{array}{ccc}
2 &-1& 0\\
1 &-2 & 1\\
0...
...rm{, }
b=\left[\begin{array}{c} 1 0 1 \end{array}\right]
\end{displaymath}](img119.png)
![\begin{displaymath}
A=
\left[
\begin{array}{ccc}
2+2i &-1& 0\\
-1 &2-2i& -1...
... }
b=\left[\begin{array}{c} 1+i 0 1-i \end{array}\right]
\end{displaymath}](img124.png)
Rodrigo Maia 2003-10-07