12.1 Produto Escalar '*'

Vamos começar por analisar qual o significado que pode ser atribuído ao produto de dois vectores. Existem dois tipos de produtos entre vectores, mas em ambos os casos o comprimento dos vectores tem obrigatoriamente que ser o mesmo.

O primeiro tipo de produto que vamos estudar é a produto escalar. Suponha que $\vec{u}$ e $\vec{v}$ são dois vectores com o mesmo comprimento $n$, sendo que $\vec{u}$ é um vector linha e $\vec{v}$ é um vector coluna:

$$\begin{eqnarray*} \vec{u} = \left[u_1,u_2,\ldots,u_n\right] & & \vec{v} = \lef... ...rray}{c} v_1 \\ v_2 \\ \vdots \\ v_n \end{array} \right] \end{eqnarray*}$$

o resultado do produto escalar é um escalar que resulta do somatório dos produtos das componentes homologas em ambos os vectores:

$$\begin{eqnarray*} \vec{u}\vec{v} &=& \sum_{i=1}^{n}u_iv_i\mathrm{.} \end{eqnarray*}$$

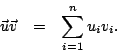
Por exemplo se $\vec{u}=\left[10,-11,12\right]$ e $\vec{v} = \left[\begin{array}{c}20 -21 -22\end{array}\right]$ e $n=3$ então:

$$\begin{eqnarray*} \vec{u}\vec{v} &=& 10\times20+(-11)\times(-21)+12\times(-22)=167\mathrm{.} \end{eqnarray*}$$

Com o Matlab este produto é realizado com os seguintes comandos:

  » u=[10,-11,12], v=[20;-21;-22]
  » prod=u*v % vector linha vezes vector coluna

No entanto, se tentarmos multiplicar um vector linha(coluna) por outro vector linha(coluna) resultará um erro:

  » prod=u*v' % vector linha vezes vector coluna transposto, que é um vector linha.
  ???? Error using ==> *
  Inner matrix dimensions must agree.

Um conceito importante dos vectores é o seu comprimento Euclidiano ou norma do vector que é representado por $\Vert\vec{u}\Vert$ e definido através:

$$\begin{eqnarray*} \Vert\vec{u}\Vert&=&\sqrt{\sum_{i=1}^{n}\vert u_i\vert^2} \end{eqnarray*}$$

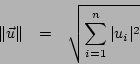
Com o Matlab isto pode ser calculado de duas formas:

  » [ sqrt(u*u'), norm(u)]
  ans =
     19.1050    19.1050

sendo que 'norm' é uma função interna do Matlab usada para calcular normas de vectores (utilize 'help norm' para ver como calcular outras normas).

Exercício 12.1   O ângulo $\theta$ entre dois vectores coluna $\vec{x}$ e $\vec{y}$ é definido como:

$$\theta=\arccos\left(\frac{\vec{x}'\vec{y}}{\Vert\vec{x}\Vert\vec{y}\Vert}\right)$$

Use esta formula para calcular o co-seno do ângulo entre os vectores:

$x=\left[1,2,3\right]'$ e $y=\left[3,2,1\right]'$