16 Ciclos 'for'

Em certas ocasiões é necessário repetir, várias vezes, um determinado segmento de código (mas em Matlab isto é menos frequente do que em outras linguagens de programação devido ao uso da notação ':').

Exemplo 16.1   Esboce os gráficos de 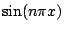$\sin(n\pi x)$ no intervalo 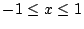$-1\leq x\leq 1$ para valores de $n=1,2,\ldots,8$.

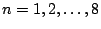Isto podia ser realizado introduzindo oito comandos 'plot' separadamente, mas é muito mais simple e fácil utilizando um ciclo 'for'. A forma mais simples seria:

» x = -1:.05:1;
» for n = 1:8
     subplot(4,2,n), plot(x,sin(n*pi*x))
   end

Todo as intruções entre as linhas começadas por 'for' e 'end' são repetidas com 'n' a tomar o valor 1 da primeira vez, 2 da segunda e por ai em diante até 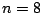$n=8$. O 'subplot' constroi uma tabela 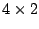$4\times 2$ de sub-janelas e, na n-ésima vez que o código é executado, um gráfico é esboçado na n-ésima sub-janela. Os comandos

» x = -1:.05:1;
» for n = 1:2:8
     subplot(4,2,n), plot(x,sin(n*pi*x))
     subplot(4,2,n+1), plot(x,cos(n*pi*x))
   end

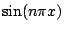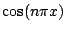desenham $\sin(n\pi x)$ e $\cos(n\pi x)$ para valores de 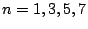$n=1,3,5,7$ uns ao lado dos outros.

Para o contador de ciclo pode ser utilizado qualquer nome de variável permitido (nos casos anteriores 'n') e este pode percorrer todos os valores de um dado vector (vector '1:8' e '1:2:8' nos exemplos anteriores. Ou seja também se pode utilizar o ciclo 'for' para ciclos do tipo:

  » for contador = [23 11 19 5.4 6]
     .......
     end

que repete as intruções pertencentes ao ciclo com a variável contador a valer 23 da primeira vez, 11 da segunda e assim sucessivamente.

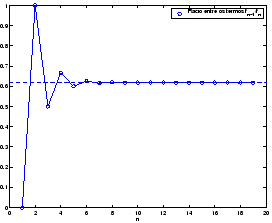
Exemplo 16.2   A sequência de Fibonnaci que começa com os números 0 e 1 e cujo os termos seguintes a são a soma dos seu dois predecessores imediatos é descrita matematicamente por:

$$f_1=0, f_2=1 \mathrm{ e } f_n=f_{n-1}+f_{n-2} \mathrm{para} n=3,4,5\ldots$$

Teste a a seguinte hipótese: o rácio entre dois termos sussecivos da sucessão de Fibonnaci (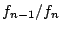$f_{n-1}/f_n$) tende para 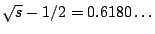$\sqrt{s}-1/2=0.6180\ldots$ à medida que 'n' aumenta.

  » F(1) = 0; F(2) = 1;
  » for i = 3:20
        F(i) = F(i-1) + F(i-2);
     end
  » plot(1:19, F(1:19)./F(2:20),'o' )
  » hold on, xlabel('n')
  » plot(1:19, F(1:19)./F(2:20),'-' )
  » legend('Racio entre os termos f_n-1/f_n')
  » plot([0 20], (sqrt(5)-1)/2*[1,1],'-')

O ultimo comando produz o a linha horizontal a tracejado.